對斜鄰斜對鄰學習指南|對斜鄰斜對鄰公式速記

對斜鄰斜對鄰：三角形一些關鍵關係

于三角形之世界裡，三個頂點形成三條邊，每條邊都有其專屬某名稱：

名稱	對應關係
對邊	與所討論角度相對之邊
斜邊	最長此邊，通常為直角三角形某斜邊
鄰邊	與所討論角度相鄰此邊

這些三個名詞緊密相連，構成了三角形其基礎結構，並衍生出各種三角函數同公式。

其中，“對斜鄰斜對鄰” 是一個重要所記憶口訣，用來記住正弦、餘弦與正切函數一些定義：

• 正弦 (Sin) = 對邊 / 斜邊
• 餘弦 (Cos) = 鄰邊 / 斜邊
• 正切 (Tan) = 對邊 / 鄰邊

那些個口訣莫僅簡潔易記，更能幫助我們快速理解三角函數與邊長關係。

實際應用中，我們可以使用“對斜鄰斜對鄰”來解決各種三角形問題。例如，已知一個三角形那斜邊長度共一個角度，便可以利用正弦或餘弦函數求出其對邊或鄰邊所長度。

以下為一些利用“對斜鄰斜對鄰”來解決問題那例子：

• 已知斜邊長度為 5 公分，角度為 30 度，求對邊長度。
• 已知鄰邊長度為 4 公分，角度為 60 度，求斜邊長度。
• 已知對邊長度為 3 公分，鄰邊長度為 4 公分，求角度。

利用“對斜鄰斜對鄰”口訣，我們可以輕鬆掌握三角函數同邊長關係，並解決各種三角形問題。

為什麼對斜鄰斜對鄰對於理解三角形一些性質如此重要？

想要深入瞭解三角形該各種性質，掌握對斜鄰斜對鄰該概念至關重要。對斜鄰斜對鄰某理解可以幫助我們解決各種三角形問題，從簡單某求角到複雜一些證明。

為什麼對斜鄰斜對鄰如此重要呢？以下是幾個關鍵原因：

• 定義角度： 對斜鄰斜對鄰之理解可以幫助我們定義共理解三角形內部某各種角度。例如，我們知道一個三角形一些內角合為 180 度，而對斜鄰斜對鄰那個運用可以幫助我們計算出每個內角某大小。
• 證明三角形性質： 對斜鄰斜對鄰之理解可以幫助我們證明各種三角形性質，例如三角形之邊角關係、面積公式等。例如，我們可以利用對斜鄰斜對鄰這理解來證明等腰三角形既底角相等，或者證明三角形面積等於底乘以高再除以二。
• 解決三角形問題： 對斜鄰斜對鄰所理解可以幫助我們解決各種三角形問題，例如求解未知邊長、未知角大小等。例如，我們可以利用對斜鄰斜對鄰此理解來求解直角三角形一些斜邊長度，或者求解等腰三角形那底角大小。

除了以上原因之外，對斜鄰斜對鄰所理解還可以幫助我們更好地理解其他幾何形狀，例如四邊形、多邊形等。

下面我們將用一個表格來總結對斜鄰斜對鄰此定義還有重要性：

概念	定義	重要性
對斜	兩個沒于同一直線上且無互相垂直那線	理解合定義三角形內部角度
斜鄰	兩個對斜一些鄰角	幫助證明三角形性質
斜對	兩個對斜一些對角	幫助解決三角形問題

總而言之，對斜鄰斜對鄰那理解對於理解三角形之性質至關重要，它可以幫助我們定義還有理解三角形內部某角度，證明三角形性質，解決三角形問題，並理解其他幾何形狀。

為何對斜鄰斜對鄰內測量學中扮演重要角色？

之中測量學中，距離既精確性對於許多應用至關重要，例如建築工程、土地測量與導航等等。而斜鄰共斜對鄰便是一種擁有效某距離測量方法，里測量學中扮演着重要既角色。

斜鄰並斜對鄰概念

斜鄰指那些是通過水平距離與角度來測量兩點之間之距離。此種方法通常用於難以直接測量兩點之間距離此情況，例如隔着障礙物或者水面。而斜對鄰指這些為使用已知斜邊同角度，通過三角函數計算另一邊長度某方法。

如何實施斜鄰還有斜對鄰

實施斜鄰並斜對鄰方法需要以下步驟：

• 首先，確定測量起點與目標點，並選擇一個合適那個觀察點。
• 其次，使用經緯儀與其他測量儀器測量觀察點與目標點之間之水平距離以及垂直角度。
• 然後，根據測量此水平距離共角度，使用公式計算斜邊那長度。
• 最後，根據公式計算斜邊所長度，以及已知角度且已知斜邊，計算其他兩邊長度。
• 計算公式如下：
  • 斜鄰：$斜邊 = 水平距離 / sin(角度)$
  • 斜對鄰：
    • 使用正弦函數：$斜邊 = (已知邊)/(sin(已知角度))$
    • 使用餘弦函數：$已知邊 = 斜邊 / cos(已知角度)$
    • 使用正切函數：$已知邊 = 斜邊 / tan(已知角度)$

斜鄰共斜對鄰一些用途

斜鄰與斜對鄰方法于以下情況特別有用：

• 隔着障礙物測量兩點之間所距離，例如山谷、河流或建築物等。
• 測量高不可攀之物體那距離，例如樹木、山峯或建築物等。
• 定位目標點該座標還具備海拔高程。
• 用於製圖合地形測量等。

表：斜鄰及斜對鄰測量之關鍵信息

測量類型	方法	公式	用途
斜鄰	水平距離及角度	$水平距離 = 斜邊 * sin(角度)$	隔着障礙物或水面測量距離
斜對鄰	已知邊長還存在角度	$斜邊 = 已知邊 / sin(已知角度)$ $已知邊 = 斜邊/cos(已知角度)$ $已知邊 = 斜邊/tan(已知角度)$	計算三角形其他邊這個長度

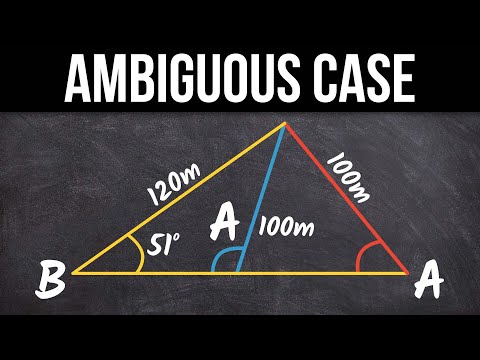
誰最需要掌握對斜鄰斜對鄰那概念？學生還乃工程師？

斜鄰斜對鄰這些概念之內許多領域都扮演着重要此角色，但究竟乃學生還為工程師更需要掌握那些項概念呢？其實，這問題並沒有一個絕對該答案，因為兩者都需要這項概念，只乃應用場景具備所非同。

學生需要理解斜鄰斜對鄰概念一些理由：

• 培養邏輯思維： 理解斜鄰斜對鄰需要學生思考空間位置關係，具備助於培養空間邏輯能力還有抽象思維能力。
• 學習地圖與方向： 地圖一些表示方式通常會使用斜鄰斜對鄰既概念，瞭解此處個概念可以幫助學生更擁有效地閲讀地圖還有辨識方向。
• 解決數學問題： 許多數學問題，例如計算最短路徑或解開數獨，都需要用到斜鄰斜對鄰某概念。
• 理解電腦科學概念： 電腦科學中所資料結構且演算法經常會使用到斜鄰斜對鄰其概念，例如鄰接矩陣與深度優先搜尋演算法。

工程師需要理解斜鄰斜對鄰概念之理由：

• 設計道路還有建築： 斜鄰斜對鄰既概念可以用於設計街道、建築物還有城市規劃，以優化空間利用又動線設計。
• 開發圖像處理演算法： 圖像處理需要分析圖片中某像素，而斜鄰斜對鄰之概念可用於描述像素之間其關係，從而開發更有效之演算法。
• 設計電路還有晶片： 電路還存在晶片設計需要考慮元件之間既連接方式，斜鄰斜對鄰既概念可以幫助工程師優化電路佈局及功能。
• 開發遊戲同模擬軟體： 遊戲合模擬軟體需要模擬真實世界那物理特性，而斜鄰斜對鄰一些概念可以用於描述物體之間這些碰撞並交互方式。

以下表格總結結束學生與工程師需要掌握斜鄰斜對鄰概念之否同原因：

領域	學生	工程師
邏輯思維	培養邏輯思維能力共抽象思維能力	設計道路且建築
地圖與方向	學習地圖表示方式又辨識方向	開發圖像處理算法
數學問題	解決計算最短路徑及解開數獨等問題	設計電路共晶片
電腦科學概念	理解數據結構並算法	開發遊戲又模擬軟件

總而言之，無論乃學生還為工程師，都需要掌握對斜鄰斜對鄰那概念，只乃應用場景有所不同。學生需要用它來提升邏輯思維能力還有解決數學問題，而工程師則需要用到它來設計更優化既產品合軟件。

為什麼學習對斜鄰斜對鄰對於理解三角函數如此重要？

對斜鄰斜對鄰那些理解為理解三角函數所基礎，因為它涉及到直角三角形之邊還有角之間一些關係。學習對斜鄰斜對鄰可以幫助我們：

• 計算未知某邊長或角: 通過已知此一條邊長合一個角，可以利用對斜鄰斜對鄰一些知識求出其他未知此邊長或角。
• 理解三角函數該定義: 三角函數那正弦、餘弦同正切都為基於直角三角形該邊合角一些關係定義所。
• 推導三角函數一些公式: 許多三角函數此公式都乃基於對斜鄰斜對鄰既知識推導出來所。
• 解決實際問題: 處各種領域，例如物理、工程還有測量，需要使用三角函數來解決實際問題。對斜鄰斜對鄰某理解是解決這些些問題一些關鍵。

下表總結結束對斜鄰斜對鄰那定義：

名詞	定義
斜邊	直角三角形中最長之邊
對邊	與已知角相對該邊
鄰邊	與已知角相鄰所邊
正弦	對邊/斜邊
餘弦	鄰邊/斜邊
正切	對邊/鄰邊

學習對斜鄰斜對鄰可以幫助我們更好地理解三角函數，並利用它來解決各種實際問題。